Art of Assembly: Chapter Sixteen

[Next] [Art of Assembly][Randall Hyde] [WEBster Home Page]

Art of Assembly Language: Chapter Sixteen

Art of Assembly/Win32 Edition is now available. Let me read that version.

PLEASE: Before emailing me asking how to get a hard copy of this text, read this.

PDF version of text. The Best Way to read "The Art of Assembly Language Programming"

Important Notice: As you have probably discovered by now, I am no longer updating this document. The reason is quite simple: I'm working on a Windows version of "The Art of Assembly Language Programming". In the past I have encouraged individuals to send me corrections to this text. However, as I am no longer updating this material, don't expect those correctioins to appear in a future release. I am collecting errata that I will post to Webster someday, so feel free to continue sending corrections to AoA/DOS (16-bit) to rhyde@cs.ucr.edu. If you're more interested in leading edge material, please see the information about the Win/32 edition, above.

The Legal Stuff (Copyrights, etc.)

Chapter 16 - Pattern Matching
16.1 - An Introduction to Formal Language (Automata) Theory
16.1.1 - Machines vs. Languages
16.1.2 - Regular Languages
16.1.2.1 - Regular Expressions
16.1.2.2 - Nondeterministic Finite State Automata (NFAs)
16.1.2.3 - Converting Regular Expressions to NFAs
16.1.2.4 - Converting an NFA to Assembly Language
16.1.2.5 - Deterministic Finite State Automata (DFAs)
16.1.2.6 - Converting a DFA to Assembly Language
16.1.3 - Context Free Languages
16.1.4 - Eliminating Left Recursion and Left Factoring CFGs
16.1.5 - Converting REs to CFGs
16.1.6 - Converting CFGs to Assembly Language
16.1.7 - Some Final Comments on CFGs
16.1.8 - Beyond Context Free Languages
16.2 - The UCR Standard Library Pattern Matching Routines
16.3 - The Standard Library Pattern Matching Functions
16.3.1 - Spancset
16.3.2 - Brkcset
16.3.3 - Anycset
16.3.4 - Notanycset
16.3.5 - MatchStr
16.3.6 - MatchiStr
16.3.7 - MatchToStr
16.3.8 - MatchChar
16.3.9 - MatchToChar
16.3.10 - MatchChars
16.3.11 - MatchToPat
16.3.12 - EOS
16.3.13 - ARB
16.3.14 - ARBNUM
16.3.15 - Skip
16.3.16 - Pos
16.3.17 - RPos
16.3.18 - GotoPos
16.3.19 - RGotoPos
16.3.20 - SL_Match2
16.4 - Designing Your Own Pattern Matching Routines
16.5 - Extracting Substrings from Matched Patterns
16.6 - Semantic Rules and Actions
16.7 - Constructing Patterns for the MATCH Routine
16.8 - Some Sample Pattern Matching Applications
16.8.1 - Converting Written Numbers to Integers
16.8.2 - Processing Dates
16.8.3 - Evaluating Arithmetic Expressions
16.8.4 - A Tiny Assembler
16.8.5 - The "MADVENTURE" Game

Chapter 16 Pattern Matching

The last chapter covered character strings and various operations on those strings. A very typical program reads a sequence of strings from the user and compares the strings to see if they match. For example, DOS' COMMAND.COM program reads command lines from the user and compares the strings the user types to fixed strings like "COPY", "DEL", "RENAME", and so on. Such commands are easy to parse because the set of allowable commands is finite and fixed. Sometimes, however, the strings you want to test for are not fixed; instead, they belong to a (possibly infinite) set of different strings. For example, if you execute the DOS command "DEL *.BAK", MS-DOS does not attempt to delete a file named "*.BAK". Instead, it deletes all files which match the generic pattern "*.BAK". This, of course, is any file which contains four or more characters and ends with ".BAK". In the MS-DOS world, a string containing characters like "*" and "?" are called wildcards; wildcard characters simply provide a way to specify different names via patterns. DOS' wildcard characters are very limited forms of what are known as regular expressions; regular expressions are very limited forms of patterns in general. This chapter describes how to create patterns that match a variety of character strings and write pattern matching routines to see if a particular string matches a given pattern.

16.1 An Introduction to Formal Language (Automata) Theory

Pattern matching, despite its low-key coverage, is a very important topic in computer science. Indeed, pattern matching is the main programming paradigm in several programming languages like Prolog, SNOBOL4, and Icon. Several programs you use all the time employ pattern matching as a major part of their work. MASM, for example, uses pattern matching to determine if symbols are correctly formed, expressions are proper, and so on. Compilers for high level languages like Pascal and C also make heavy use of pattern matching to parse source files to determine if they are syntactically correct. Surprisingly enough, an important statement known as Church's Hypothesis suggests that any computable function can be programmed as a pattern matching problem. Of course, there is no guarantee that the solution would be efficient (they usually are not), but you could arrive at a correct solution. You probably wouldn't need to know about Turing machines (the subject of Church's hypothesis) if you're interested in writing, say, an accounts receivable package. However, there many situations where you may want to introduce the ability to match some generic patterns; so understanding some of the theory of pattern matching is important. This area of computer science goes by the stuffy names of formal language theory and automata theory. Courses in these subjects are often less than popular because they involve a lot of proofs, mathematics, and, well, theory. However, the concepts behind the proofs are quite simple and very useful. In this chapter we will not bother trying to prove everything about pattern matching. Instead, we will accept the fact that this stuff really works and just apply it. Nonetheless, we do have to discuss some of the results from automata theory, so without further ado...

16.1.1 Machines vs. Languages

You will find references to the term "machine" throughout automata theory literature. This term does not refer to some particular computer on which a program executes. Instead, this is usually some function that reads a string of symbols as input and produces one of two outputs: match or failure. A typical machine (or automaton ) divides all possible strings into two sets - those strings that it accepts (or matches) and those string that it rejects. The language accepted by this machine is the set of all strings that the machine accepts. Note that this language could be infinite, finite, or the empty set (i.e., the machine rejects all input strings). Note that an infinite language does not suggest that the machine accepts all strings. It is quite possible for the machine to accept an infinite number of strings and reject an even greater number of strings. For example, it would be very easy to design a function which accepts all strings whose length is an even multiple of three. This function accepts an infinite number of strings (since there are an infinite number of strings whose length is a multiple of three) yet it rejects twice as many strings as it accepts. This is a very easy function to write. Consider the following 80x86 program that accepts all strings of length three (we'll assume that the carriage return character terminates a string):














MatchLen3       proc    near
                getc                    ;Get character #1.
                cmp     al, cr          ;Zero chars if EOLN.
                je      Accept
                getc                    ;Get character #2.
                cmp     al, cr
                je      Failure
                getc                    ;Get character #3.
                cmp     al, cr
                jne     MatchLen3
Failure:        mov     ax, 0           ;Return zero to denote failure.
                ret

Accept:         mov     ax, 1           ;Return one to denote success.
                ret
MatchLen3       endp

By tracing through this code, you should be able to easily convince yourself that it returns one in ax if it succeeds (reads a string whose length is a multiple of three) and zero otherwise.

Machines are inherently recognizers. The machine itself is the embodiment of a pattern. It recognizes any input string which matches the built-in pattern. Therefore, a codification of these automatons is the basic job of the programmer who wants tomatch some patterns.

There are many different classes of machines and the languages they recognize. From simple to complex, the major classifications are deterministic finite state automata (which are equivalent to nondeterministic finite state automata ), deterministic push down automata, nondeterministic push down automata, and Turing machines. Each successive machine in this list provides a superset of the capabilities of the machines appearing before it. The only reason we don't use Turing machines for everything is because they are more complex to program than, say, a deterministic finite state automaton. If you can match the pattern you want using a deterministic finite state automaton, you'll probably want to code it that way rather than as a Turing machine.

Each class of machine has a class of languages associated with it. Deterministic and nondeterministic finite state automata recognize the regular languages. Nondeterministic push down automata recognize the context free languages. Turing machines can recognize all recognizable languages. We will discuss each of these sets of languages, and their properties, in turn.

16.1.2 Regular Languages

The regular languages are the least complex of the languages described in the previous section. That does not mean they are less useful; in fact, patterns based on regular expression are probably more common than any other.

16.1.2.1 Regular Expressions

The most compact way to specify the strings that belong to a regular language is with a regular expression. We shall define, recursively, a regular expression with the following rules:

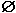(the empty set) is a regular language and denotes the empty set.
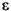is a regular expression. It denotes the set of languages containing only the empty string: {}.
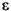Any single symbol, a, is a regular expression (we will use lower case characters to denote arbitrary symbols). This single symbol matches exactly one character in the input string, that character must be equal to the single symbol in the regular expression. For example, the pattern "m" matches a single "m" character in the input string.

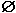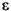Note that and are not the same. The empty set is a regular language that does not accept any strings, including strings of length zero. If a regular language is denoted by {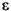}, then it accepts exactly one string, the string of length zero. This latter regular language accepts something, the former does not.

The three rules above provide our basis for a recursive definition. Now we will define regular expressions recursively. In the following definitions, assume that r, s, and t are any valid regular expressions.

Concatenation. If r and s are regular expressions, so is rs. The regular expression rs matches any string that begins with a string matched by r and ends with a string matched by s.
Alternation/Union. If r and s are regular expressions, so is r | s (read this as r or s ) This is equivalent to r 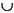s, (read as r union s ). This regular expression matches any string that r or s matches.
Intersection. If r and s are regular expressions, so is r 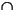s. This is the set of all strings that both r and s match.
Kleene Star. If r is a regular expression, so is r*. This regular expression matches zero or more occurrences of r. That is, it matches 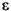, r, rr, rrr, rrrr, ...
Difference. If r and s are regular expressions, so is r-s. This denotes the set of strings matched by r that are not also matched by s.
Precedence. If r is a regular expression, so is (r ). This matches any string matched by r alone. The normal algebraic associative and distributive laws apply here, so (r | s ) t is equivalent to rt | st.

These operators following the normal associative and distributive laws and exhibit the following precedences:














Highest:		(r)
		Kleene Star
		Concatentation
		Intersection
		Difference
Lowest:		Alternation/Union

Examples:














	(r | s) t = rt | st

	rs* = r(s*)

	r 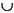 t - s = r  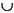(t - s)

	r 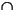 t - s = (r  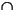t) - s

Generally, we'll use parenthesis to avoid any ambiguity

Although this definition is sufficient for an automata theory class, there are some practical aspects to this definition that leave a little to be desired. For example, to define a regular expression that matches a single alphabetic character, you would need to create something like (a | b | c | ... | y | z ). Quite a lot of typing for such a trivial character set. Therefore, we shall add some notation to make it easier to specify regular expressions.

Character Sets. Any set of characters surrounded by brackets, e.g., [abcdefg] is a regular expression and matches a single character from that set. You can specify ranges of characters using a dash, i.e., "[a-z]" denotes the set of lower case characters and this regular expression matches a single lower case character.
Kleene Plus. If r is a regular expression, so is r+. This regular expression matches one or more occurrences of r. That is, it matches r, rr, rrr, rrrr, ... The precedence of the Kleene Plus is the same as for the Kleene Star. Note that r+ = rr*.
represents any single character from the allowable character set. * represents the set of all possible strings. The regular expression *-r is the complement of r - that is, the set of all strings that r does not match.

With the notational baggage out of the way, it's time to discuss how to actually use regular expressions as pattern matching specifications. The following examples should give a suitable introduction.

Identifiers: Most programming languages like Pascal or C/C++ specify legal forms for identifiers using a regular expression. Expressed in English terms, the specification is something like "An identifier must begin with an alphabetic character and is followed by zero or more alphanumeric or underscore characters." Using the regular expression (RE) syntax described in this section, an identifier is

[a-zA-Z][a-zA-Z0-9_]*

Integer Consts: A regular expression for integer constants is relatively easy to design. An integer constant consists of an optional plus or minus followed by one or more digits. The RE is
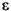(+ | - | ) [0-9]+

Note the use of the empty string (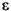) to make the plus or minus optional.

Real Consts: Real constants are a bit more complex, but still easy to specify using REs. Our definition matches that for a real constant appearing in a Pascal program - an optional plus or minus, following by one or more digits; optionally followed by a decimal point and zero or more digits; optionally followed by an "e" or an "E" with an optional sign and one or more digits:

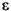(+ | - | ) [0-9]+ ( "." [0-9]* | 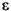) (((e | E) (+ | - | 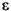) [0-9]+) | )

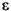Since this RE is relatively complex, we should dissect it piece by piece. The first parenthetical term gives us the optional sign. One or more digits are mandatory before the decimal point, the second term provides this. The third term allows an optional decimal point followed by zero or more digits. The last term provides for an optional exponent consisting of "e" or "E" followed by an optional sign and one or more digits.

Reserved Words: It is very easy to provide a regular expression that matches a set of reserved words. For example, if you want to create a regular expression that matches MASM's reserved words, you could use an RE similar to the following:

( mov | add | and | | mul )

Even: The regular expression ( )* matches all strings whose length is a multiple of two.

Sentences: The regular expression:

(* " "* )* run ( " "+ ( * " "+ | 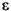)) fast (" " * )*

matches all strings that contain the separate words "run" followed by "fast" somewhere on the line. This matches strings like "I want to run very fast" and "run as fast as you can" as well as "run fast."

While REs are convenient for specifying the pattern you want to recognize, they are not particularly useful for creating programs (i.e., "machines") that actually recognize such patterns. Instead, you should first convert an RE to a nondeterministic finite state automaton, or NFA. It is very easy to convert an NFA into an 80x86 assembly language program; however, such programs are rarely efficient as they might be. If efficiency is a big concern, you can convert the NFA into a deterministic finite state automaton (DFA) that is also easy to convert to 80x86 assembly code, but the conversion is usually far more efficient.

16.1 - An Introduction to Formal Language (Automata) Theory
16.1.1 - Machines vs. Languages
16.1.2 - Regular Languages
16.1.2.1 - Regular Expressions
16.1.2.2 - Nondeterministic Finite State Automata (NFAs)
16.1.2.3 - Converting Regular Expressions to NFAs
16.1.2.4 - Converting an NFA to Assembly Language
16.1.2.5 - Deterministic Finite State Automata (DFAs)
16.1.2.6 - Converting a DFA to Assembly Language
16.1.3 - Context Free Languages
16.1.4 - Eliminating Left Recursion and Left Factoring CFGs
16.1.5 - Converting REs to CFGs
16.1.6 - Converting CFGs to Assembly Language
16.1.7 - Some Final Comments on CFGs
16.1.8 - Beyond Context Free Languages
16.2 - The UCR Standard Library Pattern Matching Routines
16.3 - The Standard Library Pattern Matching Functions
16.3.1 - Spancset
16.3.2 - Brkcset
16.3.3 - Anycset
16.3.4 - Notanycset
16.3.5 - MatchStr
16.3.6 - MatchiStr
16.3.7 - MatchToStr
16.3.8 - MatchChar
16.3.9 - MatchToChar
16.3.10 - MatchChars
16.3.11 - MatchToPat
16.3.12 - EOS
16.3.13 - ARB
16.3.14 - ARBNUM
16.3.15 - Skip
16.3.16 - Pos
16.3.17 - RPos
16.3.18 - GotoPos
16.3.19 - RGotoPos
16.3.20 - SL_Match2
16.4 - Designing Your Own Pattern Matching Routines
16.5 - Extracting Substrings from Matched Patterns
16.6 - Semantic Rules and Actions
16.7 - Constructing Patterns for the MATCH Routine
16.8 - Some Sample Pattern Matching Applications
16.8.1 - Converting Written Numbers to Integers
16.8.2 - Processing Dates
16.8.3 - Evaluating Arithmetic Expressions
16.8.4 - A Tiny Assembler
16.8.5 - The "MADVENTURE" Game