repeat...until allow nesting and are always balanced (e.g., for every repeat there is a corresponding until statement later in the source file).
. Context free grammars use nonterminal symbols for function calls and definitions. In our context free grammars we will use italic characters to denote nonterminal symbols and standard characters to denote terminal symbols.
expression + factor. The first plus sign suggests that the expression term must match "7" and the factor term must match "5*(2+1)". Now we need to match our input string with the pattern expression + factor. To do this, we call the expression function once again, this time using the expression factor production. This give us the reduction:
expression + factor factor + factor symbol denotes the application of a nonterminal function call (a reduction).term to yield the reduction:expression + factor factor + factor term + factor expression + factor factor + factor term + factor IntegerConstant + factor expression + factor factor + factor term + factor IntegerConstant + factor 7 + factor expression
The final reduction completes the derivation of our input string, so the string 7+5*(2+1) is in the language specified by the context free grammar.
expression
Such a conversion would yield some assembly code that looks roughly like the following:
expression proc near
call expression
jnc fail
cmp byte ptr es:[di], '+'
jne fail
inc di
call factor
jnc fail
stc
ret
Fail: clc
ret
expression endp
The obvious problem with this code is that it will generate an infinite loop. Upon entering the expression function this code immediately calls expression recursively, which immediately calls expression recursively, which immediately calls expression recursively, ... Clearly, we need to resolve this problem if we are going to write any real code to match this production.
The trick to resolving left recursion is to note that if there is a production that suffers from left recursion, there must be some production with the same left hand side that is not left recursive. All we need do is rewrite the left recursive call in terms of the production that does not have any left recursion. This sound like a difficult task, but it's actually quite easy.
To see how to eliminate left recursion, let Xi and Yj represent any set of terminal symbols or nonterminal symbols that do not have a right hand side beginning with the nonterminal A. If you have some productions of the form:
A
You will be able to translate this to an equivalent grammar without left recursion by replacing each term of the form A Yi by A Yi A and each term of the form A AXi by A' Xi A' | . For example, consider three of the productions from the arithmetic grammar:
expression
In this example A corresponds to expression, X1 corresponds to "+ factor ", X2 corresponds to "- factor ", and Y1 corresponds to "factor ". The equivalent grammar without left recursion is
expression
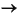
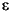
The complete arithmetic grammar, with left recursion removed, is
expression
Another useful transformation on a grammar is to left factor the grammar. This can reduce the need for backtracking, improving the performance of your pattern matching code. Consider the following CFG fragment:
stmt
These two productions begin with the same set of symbols. Either production will match all the characters in an if statement up to the point the matching algorithm encounters the first else or endif. If the matching algorithm processes the first statement up to the point of the endif terminal symbol and encounters the else terminal symbol instead, it must backtrack all the way to the if symbol and start over. This can be terribly inefficient because of the recursive call to stmt (imagine a 10,000 line program that has a single if statement around the entire 10,000 lines, a compiler using this pattern matching technique would have to recompile the entire program from scratch if it used backtracking in this fashion). However, by left factoring the grammar before converting it to program code, you can eliminate the need for backtracking.
To left factor a grammar, you collect all productions that have the same left hand side and begin with the same symbols on the right hand side. In the two productions above, the common symbols are "if expression then stmt ". You combine the common strings into a single production and then append a new nonterminal symbol to the end of this new production, e.g.,
stmt
Finally, you create a new set of productions using this new nonterminal for each of the suffixes to the common production:
NewNonTerm
This eliminates backtracking because the matching algorithm can process the if, the expression, the then, and the stmt before it has to choose between endif and else.
xyz. This applies equally to the empty string, .R S.R | S.R RStar | .R RPlus | R.TR SStarSStar
Likewise, to handle a grammar of the form (RS )* you could use productions of the form:
TR S T |R S
es:di always points at the start of the string we want to match. The second convention we will adopt is to create a function for each nonterminal. This function returns success (carry set) if it matches an associated subpattern, it returns failure (carry clear) otherwise. If it succeeds, it leaves di pointing at the next character is the staring after the matched pattern; if it fails, it preserves the value in di across the function call.T and there are no other productions associated with T, then this production always succeeds. The corresponding assembly code is simply:
T proc near
stc
ret
T endp
Of course, there is no real need to ever call T and test the returned result since we know it will always succeed. On the other hand, if T is a stub that you intend to fill in later, you should call T.
If a production takes the form T xyz, where xyz is a string of one or more terminal symbols, then the function returns success if the next several input characters match xyz, it returns failure otherwise. Remember, if the prefix of the input string matches xyz, then the matching function must advance di beyond these characters. If the first characters of the input string does not match xyz, it must preserve di. The following routines demonstrate two cases, where xyz is a single character and where xyz is a string of characters:
T1 proc near
cmp byte ptr es:[di], 'x' ;Single char.
je Success
clc ;Return Failure.
ret
Success: inc di ;Skip matched char.
stc ;Return success.
ret
T1 endp
T2 proc near
call MatchPrefix
byte 'xyz',0
ret
T2 endp
MatchPrefix is a routine that matches the prefix of the string pointed at by es:di against the string following the call in the code stream. It returns the carry set and adjusts di if the string in the code stream is a prefix of the input string, it returns the carry flag clear and preserves di if the literal string is not a prefix of the input. The MatchPrefix code follows:
MatchPrefix proc far ;Must be far!
push bp
mov bp, sp
push ax
push ds
push si
push di
lds si, 2[bp] ;Get the return address.
CmpLoop: mov al, ds:[si] ;Get string to match.
cmp al, 0 ;If at end of prefix,
je Success ; we succeed.
cmp al, es:[di] ;See if it matches prefix,
jne Failure ; if not, immediately fail.
inc si
inc di
jmp CmpLoop
Success: add sp, 2 ;Don't restore di.
inc si ;Skip zero terminating byte.
mov 2[bp], si ;Save as return address.
pop si
pop ds
pop ax
pop bp
stc ;Return success.
ret
Failure: inc si ;Need to skip to zero byte.
cmp byte ptr ds:[si], 0
jne Failure
inc si
mov 2[bp], si ;Save as return address.
pop di
pop si
pop ds
pop ax
pop bp
clc ;Return failure.
ret
MatchPrefix endp
If a production takes the form T R, where R is a nonterminal, then the T function calls R and returns whatever status R returns, e.g.,
T proc near call R ret T endp
If the right hand side of a production contains a string of terminal and nonterminal symbols, the corresponding assembly code checks each item in turn. If any check fails, then the function returns failure. If all items succeed, then the function returns success. For example, if you have a production of the form T R abc S you could implement this in assembly language as
T proc near
push di ;If we fail, must preserve di.
call R
jnc Failure
call MatchPrefix
byte "abc",0
jnc Failure
call S
jnc Failure
add sp, 2 ;Don't preserve di if we succeed.
stc
ret
Failure: pop di
clc
ret
T endp
Note how this code preserves di if it fails, but does not preserve di if it succeeds.
If you have multiple productions with the same left hand side (i.e., alternation), then writing an appropriate matching function for the productions is only slightly more complex than the single production case. If you have multiple productions associated with a single nonterminal on the left hand side, then create a sequence of code to match each of the individual productions. To combine them into a single matching function, simply write the function so that it succeeds if any one of these code sequences succeeds. If one of the productions is of the form T e, then test the other conditions first. If none of them could be selected, the function succeeds. For example, consider the productions:
E'
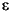
This translates to the following assembly code:
EPrime proc near
push di
cmp byte ptr es:[di], '+'
jne TryMinus
inc di
call factor
jnc EP_Failed
call EPrime
jnc EP_Failed
Success: add sp, 2
stc
ret
TryMinus: cmp byte ptr es:[di], '-'
jne EP_Failed
inc di
call factor
jnc EP_Failed
call EPrime
jnc EP_Failed
add sp, 2
stc
ret
EP_Failed: pop di
stc ;Succeed because of E' -> e
ret
EPrime endp
This routine always succeeds because it has the production E' . This is why the stc instruction appears after the EP_Failed label.
To invoke a pattern matching function, simply load es:di with the address of the string you want to test and call the pattern matching function. On return, the carry flag will contain one if the pattern matches the string up to the point returned in di. If you want to see if the entire string matches the pattern, simply check to see if es:di is pointing at a zero byte when you get back from the function call. If you want to see if a string belongs to a context free language, you should call the function associated with the starting symbol for the given context free grammar.
The following program implements the arithmetic grammar we've been using as examples throughout the past several sections. The complete implementation is
; ARITH.ASM
;
; A simple recursive descent parser for arithmetic strings.
.xlist
include stdlib.a
includelib stdlib.lib
.list
dseg segment para public 'data'
; Grammar for simple arithmetic grammar (supports +, -, *, /):
;
; E -> FE'
; E' -> + F E' | - F E' | <empty string>
; F -> TF'
; F' -> * T F' | / T F' | <empty string>
; T -> G | (E)
; G -> H | H G
; H -> 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
;
InputLine byte 128 dup (0)
dseg ends
cseg segment para public 'code'
assume cs:cseg, ds:dseg
; Matching functions for the grammar.
; These functions return the carry flag set if they match their
; respective item. They return the carry flag clear if they fail.
; If they fail, they preserve di. If they succeed, di points to
; the first character after the match.
; E -> FE'
E proc near
push di
call F ;See if F, then E', succeeds.
jnc E_Failed
call EPrime
jnc E_Failed
add sp, 2 ;Success, don't restore di.
stc
ret
E_Failed: pop di ;Failure, must restore di.
clc
ret
E endp
; E' -> + F E' | - F E' | e
EPrime proc near
push di
; Try + F E' here
cmp byte ptr es:[di], '+'
jne TryMinus
inc di
call F
jnc EP_Failed
call EPrime
jnc EP_Failed
Success: add sp, 2
stc
ret
; Try - F E' here.
TryMinus: cmp byte ptr es:[di], '-'
jne Success
inc di
call F
jnc EP_Failed
call EPrime
jnc EP_Failed
add sp, 2
stc
ret
; If none of the above succeed, return success anyway because we have
; a production of the form E' -> e.
EP_Failed: pop di
stc
ret
EPrime endp
; F -> TF'
F proc near
push di
call T
jnc F_Failed
call FPrime
jnc F_Failed
add sp, 2 ;Success, don't restore di.
stc
ret
F_Failed: pop di
clc
ret
F endp
; F -> * T F' | / T F' | e
FPrime proc near
push di
cmp byte ptr es:[di], '*' ;Start with "*"?
jne TryDiv
inc di ;Skip the "*".
call T
jnc FP_Failed
call FPrime
jnc FP_Failed
Success: add sp, 2
stc
ret
; Try F -> / T F' here
TryDiv: cmp byte ptr es:[di], '/' ;Start with "/"?
jne Success ;Succeed anyway.
inc di ;Skip the "/".
call T
jnc FP_Failed
call FPrime
jnc FP_Failed
add sp, 2
stc
ret
; If the above both fail, return success anyway because we've got
; a production of the form F -> e
FP_Failed: pop di
stc
ret
FPrime endp
; T -> G | (E)
T proc near
; Try T -> G here.
call G
jnc TryParens
ret
; Try T -> (E) here.
TryParens: push di ;Preserve if we fail.
cmp byte ptr es:[di], '(' ;Start with "("?
jne T_Failed ;Fail if no.
inc di ;Skip "(" char.
call E
jnc T_Failed
cmp byte ptr es:[di], ')' ;End with ")"?
jne T_Failed ;Fail if no.
inc di ;Skip ")"
add sp, 2 ;Don't restore di,
stc ; we've succeeded.
ret
T_Failed: pop di
clc
ret
T endp
; The following is a free-form translation of
;
; G -> H | H G
; H -> 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
;
; This routine checks to see if there is at least one digit. It fails if there
; isn't at least one digit; it succeeds and skips over all digits if there are
; one or more digits.
G proc near
cmp byte ptr es:[di], '0' ;Check for at least
jb G_Failed ; one digit.
cmp byte ptr es:[di], '9'
ja G_Failed
DigitLoop: inc di ;Skip any remaining
cmp byte ptr es:[di], '0' ; digits found.
jb G_Succeeds
cmp byte ptr es:[di], '9'
jbe DigitLoop
G_Succeeds: stc
ret
G_Failed: clc ;Fail if no digits
ret ; at all.
G endp
; This main program tests the matching functions above and demonstrates
; how to call the matching functions.
Main proc
mov ax, seg dseg ;Set up the segment registers
mov ds, ax
mov es, ax
printf
byte "Enter an arithmetic expression: ",0
lesi InputLine
gets
call E
jnc BadExp
; Good so far, but are we at the end of the string?
cmp byte ptr es:[di], 0
jne BadExp
; Okay, it truly is a good expression at this point.
printf
byte "'%s' is a valid expression",cr,lf,0
dword InputLine
jmp Quit
BadExp: printf
byte "'%s' is an invalid arithmetic expression",cr,lf,0
dword InputLine
Quit: ExitPgm
Main endp
cseg ends
sseg segment para stack 'stack'
stk byte 1024 dup ("stack ")
sseg ends
zzzzzzseg segment para public 'zzzzzz'
LastBytes byte 16 dup (?)
zzzzzzseg ends
end Main