4.2.6 Extended Precision NEG Operations
Although there are several ways to negate an extended precision value, the shortest way for smaller values (96 bits or less) is to use a combination of NEG and SBB instructions. This technique uses the fact that NEG subtracts its operand from zero. In particular, it sets the flags the same way the SUB instruction would if you subtracted the destination value from zero. This code takes the following form (assuming you want to negate the 64-bit value in EDX:EAX):
neg( edx ); neg( eax ); sbb( 0, edx );The SBB instruction decrements EDX if there is a borrow out of the L.O. word of the negation operation (which always occurs unless EAX is zero).
To extend this operation to additional bytes, words, or double words is easy; all you have to do is start with the H.O. memory location of the object you want to negate and work towards the L.O. byte. The following code computes a 128 bit negation:
static Value: dword[4]; . . . neg( Value[12] ); // Negate the H.O. double word. neg( Value[8] ); // Neg previous dword in memory. sbb( 0, Value[12] ); // Adjust H.O. dword. neg( Value[4] ); // Negate the second dword in the object. sbb( 0, Value[8] ); // Adjust third dword in object. sbb( 0, Value[12] ); // Adjust the H.O. dword. neg( Value ); // Negate the L.O. dword. sbb( 0, Value[4] ); // Adjust second dword in object. sbb( 0, Value[8] ); // Adjust third dword in object. sbb( 0, Value[12] ); // Adjust the H.O. dword.Unfortunately, this code tends to get really large and slow since you need to propagate the carry through all the H.O. words after each negate operation. A simpler way to negate larger values is to simply subtract that value from zero:
static Value: dword[5]; // 160-bit value. . . . mov( 0, eax ); sub( Value, eax ); mov( eax, Value ); mov( 0, eax ); sbb( Value[4], eax ); mov( eax, Value[4] ); mov( 0, eax ); sbb( Value[8], eax ); mov( eax, Value[8] ); mov( 0, eax ); sbb( Value[12], eax ); mov( eax, Value[12] ); mov( 0, eax ); sbb( Value[16], eax ); mov( eax, Value[16] );4.2.7 Extended Precision AND Operations
Performing an n-byte AND operation is very easy - simply AND the corresponding bytes between the two operands, saving the result. For example, to perform the AND operation where all operands are 64 bits long, you could use the following code:
mov( (type dword source1), eax ); and( (type dword source2), eax ); mov( eax, (type dword dest) ); mov( (type dword source1[4]), eax ); and( (type dword source2[4]), eax ); mov( eax, (type dword dest[4]) );This technique easily extends to any number of words, all you need to is logically AND the corresponding bytes, words, or double words together in the operands. Note that this sequence sets the flags according to the value of the last AND operation. If you AND the H.O. double words last, this sets all but the zero flag correctly. If you need to test the zero flag after this sequence, you will need to logically OR the two resulting double words together (or otherwise compare them both against zero).
4.2.8 Extended Precision OR Operations
Multi-byte logical OR operations are performed in the same way as multi-byte AND operations. You simply OR the corresponding bytes in the two operand together. For example, to logically OR two 96 bit values, use the following code:
mov( (type dword source1), eax ); or( (type dword source2), eax ); mov( eax, (type dword dest) ); mov( (type dword source1[4]), eax ); or( (type dword source2[4]), eax ); mov( eax, (type dword dest[4]) ); mov( (type dword source1[8]), eax ); or( (type dword source2[8]), eax ); mov( eax, (type dword dest[8]) );As for the previous example, this does not set the zero flag properly for the entire operation. If you need to test the zero flag after a multiprecision OR, you must logically OR the resulting double words together.
4.2.9 Extended Precision XOR Operations
Extended precision XOR operations are performed in a manner identical to AND/OR - simply XOR the corresponding bytes in the two operands to obtain the extended precision result. The following code sequence operates on two 64 bit operands, computes their exclusive-or, and stores the result into a 64 bit variable.
mov( (type dword source1), eax ); xor( (type dword source2), eax ); mov( eax, (type dword dest) ); mov( (type dword source1[4]), eax ); xor( (type dword source2[4]), eax ); mov( eax, (type dword dest[4]) );The comment about the zero flag in the previous two sections applies here.
4.2.10 Extended Precision NOT Operations
The NOT instruction inverts all the bits in the specified operand. An extended precision NOT is performed by simply executing the NOT instruction on all the affected operands. For example, to perform a 64 bit NOT operation on the value in (edx:eax), all you need to do is execute the instructions:
not( eax ); not( edx );Keep in mind that if you execute the NOT instruction twice, you wind up with the original value. Also note that exclusive-ORing a value with all ones ($FF, $FFFF, or $FFFF_FFFF) performs the same operation as the NOT instruction.
4.2.11 Extended Precision Shift Operations
Extended precision shift operations require a shift and a rotate instruction. Consider what must happen to implement a 64 bit SHL using 32 bit operations:
1) A zero must be shifted into bit zero.
2) Bits zero through 30 are shifted into the next higher bit.
3) Bit 31 is shifted into bit 32.
4) Bits 32 through 62 must be shifted into the next higher bit.
5) Bit 63 is shifted into the carry flag.
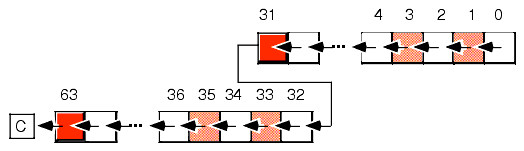
Figure 4.5 64-bit Shift Left Operation
The two instructions you can use to implement this 32 bit shift are SHL and RCL. For example, to shift the 64 bit quantity in (EDX:EAX) one position to the left, you'd use the instructions:
shl( 1, eax ); rcl( 1, eax );Note that you can only shift an extended precision value one bit at a time. You cannot shift an extended precision operand several bits using the CL register. Nor can you specify a constant value greater than one using this technique.
To understand how this instruction sequence works, consider the operation of these instructions on an individual basis. The SHL instruction shifts a zero into bit zero of the 64 bit operand and shifts bit 31 into the carry flag. The RCL instruction then shifts the carry flag into bit 32 and then shifts bit 63 into the carry flag. The result is exactly what we want.
To perform a shift left on an operand larger than 64 bits you simply add additional RCL instructions. An extended precision shift left operation always starts with the least significant word and each succeeding RCL instruction operates on the next most significant word. For example, to perform a 96 bit shift left operation on a memory location you could use the following instructions:
shl( 1, (type dword Operand[0]) ); rcl( 1, (type dword Operand[4]) ); rcl( 1, (type dword Operand[8]) );If you need to shift your data by two or more bits, you can either repeat the above sequence the desired number of times (for a constant number of shifts) or you can place the instructions in a loop to repeat them some number of times. For example, the following code shifts the 96 bit value Operand to the left the number of bits specified in ECX:
ShiftLoop: shl( 1, (type dword Operand[0]) ); rcl( 1, (type dword Operand[4]) ); rcl( 1, (type dword Operand[8]) ); dec( ecx ); jnz ShiftLoop;You implement SHR and SAR in a similar way, except you must start at the H.O. word of the operand and work your way down to the L.O. word:
// Double precision SAR: sar( 1, (type dword Operand[8]) ); rcr( 1, (type dword Operand[4]) ); rcr( 1, (type dword Operand[0]) ); // Double precision SHR: shr( 1, (type dword Operand[8]) ); rcr( 1, (type dword Operand[4]) ); rcr( 1, (type dword Operand[0]) );There is one major difference between the extended precision shifts described here and their 8/16/32 bit counterparts - the extended precision shifts set the flags differently than the single precision operations. This is because the rotate instructions affect the flags differently than the shift instructions. Fortunately, the carry is the flag most often tested after a shift operation and the extended precision shift operations (i.e., rotate instructions) properly set this flag.
The SHLD and SHRD instructions let you efficiently implement multiprecision shifts of several bits. These instructions have the following syntax:
shld( constant, Operand1, Operand2 ); shld( cl, Operand1, Operand2 ); shrd( constant, Operand1, Operand2 ); shrd( cl, Operand1, Operand2 );The SHLD instruction does the following:
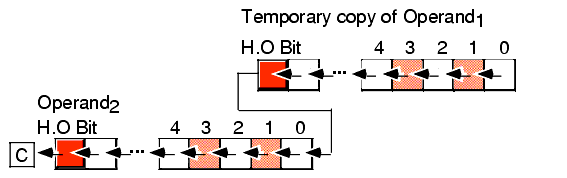
Operand1 must be a 16 or 32 bit register. Operand2 can be a register or a memory location. Both operands must be the same size. The immediate operand can be a value in the range zero through n-1, where n is the number of bits in the two operands; it specifies the number of bits to shift.
The SHLD instruction shifts bits in Operand2 to the left. The H.O. bits shift into the carry flag and the H.O. bits of Operand1 shift into the L.O. bits of Operand2. Note that this instruction does not modify the value of Operand1, it uses a temporary copy of Operand1 during the shift. The immediate operand specifies the number of bits to shift. If the count is n, then SHLD shifts bit n-1 into the carry flag. It also shifts the H.O. n bits of Operand1 into the L.O. n bits of Operand2. The SHLD instruction sets the flag bits as follows:
- If the shift count is zero, the SHLD instruction doesn't affect any flags.
- The carry flag contains the last bit shifted out of the H.O. bit of the Operand2.
- If the shift count is one, the overflow flag will contain one if the sign bit of Operand2 changes during the shift. If the count is not one, the overflow flag is undefined.
- The zero flag will be one if the shift produces a zero result.
- The sign flag will contain the H.O. bit of the result.
The SHRD instruction is similar to SHLD except, of course, it shifts its bits right rather than left. To get a clear picture of the SHRD instruction, consider Figure 4.7
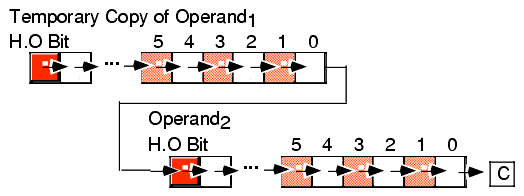
The SHRD instruction sets the flag bits as follows:
- If the shift count is zero, the SHRD instruction doesn't affect any flags.
- The carry flag contains the last bit shifted out of the L.O. bit of the Operand2.
- If the shift count is one, the overflow flag will contain one if the H.O. bit of Operand2 changes. If the count is not one, the overflow flag is undefined.
- The zero flag will be one if the shift produces a zero result.
- The sign flag will contain the H.O. bit of the result.
Consider the following code sequence:
static ShiftMe: dword[3] := [ $1234, $5678, $9012 ]; . . . mov( ShiftMe[4], eax ) shld( 6, eax, ShiftMe[8] ); mov( ShiftMe[0], eax ); shld( 6, eax, ShiftMe[4] ); shl( 6, ShiftMe[0] );The first SHLD instruction above shifts the bits from ShiftMe+4 into ShiftMe+8 without affecting the value in ShiftMe+4. The second SHLD instruction shifts the bits from SHIFTME into SHIFTME+4. Finally, the SHL instruction shifts the L.O. double word the appropriate amount. There are two important things to note about this code. First, unlike the other extended precision shift left operations, this sequence works from the H.O. double word down to the L.O. double word. Second, the carry flag does not contain the carry out of the H.O. shift operation. If you need to preserve the carry flag at that point, you will need to push the flags after the first SHLD instruction and pop the flags after the SHL instruction.
You can do an extended precision shift right operation using the SHRD instruction. It works almost the same way as the code sequence above except you work from the L.O. double word to the H.O. double word. The solution is left as an exercise.
4.2.12 Extended Precision Rotate Operations
The RCL and RCR operations extend in a manner almost identical to that for SHL and SHR . For example, to perform 96 bit RCL and RCR operations, use the following instructions:
rcl( 1, (type dword Operand[0]) ); rcl( 1, (type dword Operand[4]) ); rcl( 1, (type dword Operand[8]) ); rcr( 1, (type dword Operand[8]) ); rcr( 1, (type dword Operand[4]) ); rcr( 1, (type dword Operand[0]) );The only difference between this code and the code for the extended precision shift operations is that the first instruction is a RCL or RCR rather than a SHL or SHR instruction.
Performing an extended precision ROL or ROR instruction isn't quite as simple an operation. You can use the BT, SHLD, and SHRD instructions to implement an extended precision ROL or ROR instruction. The following code shows how to use the SHLD instruction to do an extended precision ROL:
// Compute ROL( 4, EDX:EAX ); mov( edx, ebx ); shld, 4, eax, edx ); shld( 4, ebx, eax ); bt( 0, eax ); // Set carry flag, if desired.An extended precision ROR instruction is similar; just keep in mind that you work on the L.O. end of the object first and the H.O. end last.
|