4.2.4 Extended Precision Multiplication
Although an 8x8, 16x16, or 32x32 multiply is usually sufficient, there are times when you may want to multiply larger values together. You will use the x86 single operand MUL and IMUL instructions for extended precision multiplication.
Not surprisingly (in view of how we achieved extended precision addition using ADC and SBB), you use the same techniques to perform extended precision multiplication on the x86 that you employ when manually multiplying two values. Consider a simplified form of the way you perform multi-digit multiplication by hand:
1) Multiply the first two 2) Multiply 5*2: digits together (5*3): 123 123 45 45 --- --- 15 15 10 3) Multiply 5*1: 4) Multiply 4*3: 123 123 45 45 --- --- 15 15 10 10 5 5 12 5) Multiply 4*2: 6) Multiply 4*1: 123 123 45 45 --- --- 15 15 10 10 5 5 12 12 8 8 4 7) Add all the partial products together: 123 45 --- 15 10 5 12 8 4 ------ 5535The 80x86 does extended precision multiplication in the same manner except that it works with bytes, words, and double words rather than digits. Figure 4.2 shows how this works

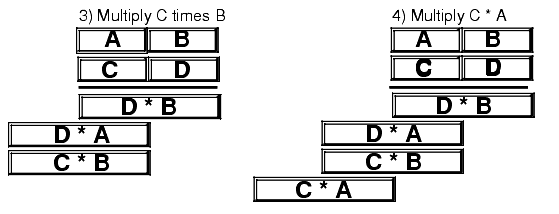
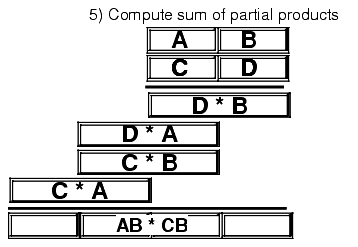
Figure 4.2 Extended Precision Multiplication
Probably the most important thing to remember when performing an extended precision multiplication is that you must also perform a multiple precision addition at the same time. Adding up all the partial products requires several additions that will produce the result. The following listing demonstrates the proper way to multiply two 64 bit values on a 32 bit processor:
Note: Multiplier and Multiplicand are 64 bit variables declared in the data segment via the qword type. Product is a 128 bit variable declared in the data segment via the qword[2] type.
program testMUL64; #include( "stdlib.hhf" ) type t128:dword[4]; procedure MUL64( Multiplier:qword; Multiplicand:qword; var Product:t128 ); const mp: text := "(type dword Multiplier)"; mc: text := "(type dword Multiplicand)"; prd:text := "(type dword [edi])"; begin MUL64; mov( Product, edi ); // Multiply the L.O. dword of Multiplier times Multiplicand. mov( mp, eax ); mul( mc, eax ); // Multiply L.O. dwords. mov( eax, prd ); // Save L.O. dword of product. mov( edx, ecx ); // Save H.O. dword of partial product result. mov( mp, eax ); mul( mc[4], eax ); // Multiply mp(L.O.) * mc(H.O.) add( ecx, eax ); // Add to the partial product. adc( 0, edx ); // Don't forget the carry! mov( eax, ebx ); // Save partial product for now. mov( edx, ecx ); // Multiply the H.O. word of Multiplier with Multiplicand. mov( mp[4], eax ); // Get H.O. dword of Multiplier. mul( mc, eax ); // Multiply by L.O. word of Multiplicand. add( ebx, eax ); // Add to the partial product. mov( eax, prd[4] ); // Save the partial product. adc( edx, ecx ); // Add in the carry! pushfd(); // Save carry out here. mov( mp[4], eax ); // Multiply the two H.O. dwords together. mul( mc[4], eax ); popfd(); // Retrieve carry from above adc( ecx, eax ); // Add in partial product from above. adc( 0, edx ); // Don't forget the carry! mov( eax, prd[8] ); // Save the partial product. mov( edx, prd[12] ); end MUL64; static op1: qword; op2: qword; rslt: t128; begin testMUL64; // Initialize the qword values (note that static objects // are initialized with zero bits). mov( 1234, (type dword op1 )); mov( 5678, (type dword op2 )); MUL64( op1, op2, rslt ); // The following only prints the L.O. qword, but // we know the H.O. qword is zero so this is okay. stdout.put( "rslt=" ); stdout.putu64( (type qword rslt)); end testMUL64; Program 4.1 Extended Precision MultiplicationOne thing you must keep in mind concerning this code, it only works for unsigned operands. To multiply two signed values you must note the signs of the operands before the multiplication, take the absolute value of the two operands, do an unsigned multiplication, and then adjust the sign of the resulting product based on the signs of the original operands. Multiplication of signed operands appears in the exercises.
This example was fairly straight-forward since it was possible to keep the partial products in various registers. If you need to multiply larger values together, you will need to maintain the partial products in temporary (memory) variables. Other than that, the algorithm that Program 4.1 uses generalizes to any number of double words.
4.2.5 Extended Precision Division
You cannot synthesize a general n-bit/m-bit division operation using the DIV and IDIV instructions. Such an operation must be performed using a sequence of shift and subtract instructions and is extremely messy. However, a less general operation, dividing an n-bit quantity by a 32 bit quantity is easily synthesized using the DIV instruction. This section presents both methods for extended precision division.
Before describing how to perform a multi-precision division operation, you should note that some operations require an extended precision division even though they may look calculable with a single DIV or IDIV instruction. Dividing a 64-bit quantity by a 32-bit quantity is easy, as long as the resulting quotient fits into 32 bits. The DIV and IDIV instructions will handle this directly. However, if the quotient does not fit into 32 bits then you have to handle this problem as an extended precision division. The trick here is to divide the (zero or sign extended) H.O dword of the dividend by the divisor, and then repeat the process with the remainder and the L.O. dword of the dividend. The following sequence demonstrates this:
static dividend: dword[2] := [$1234, 4]; // = $4_0000_1234. divisor: dword := 2; // dividend/divisor = $2_0000_091A quotient: dword[2]; remainder:dword; . . . mov( divisor, ebx ); mov( dividend[4], eax ); xor( edx, edx ); // Zero extend for unsigned division. div( ebx, edx:eax ); mov( eax, quotient[4] ); // Save H.O. dword of the quotient (2). mov( dividend[0], eax ); // Note that this code does *NOT* zero extend div( ebx, edx:eax ); // EAX into EDX before this DIV instr. mov( eax, quotient[0] ); // Save L.O. dword of the quotient ($91a). mov( edx, remainder ); // Save away the remainder.Since it is perfectly legal to divide a value by one, it is certainly possible that the resulting quotient after a division could require as many bits as the dividend. That is why the quotient variable in this example is the same size (64 bits) as the dividend variable. Regardless of the size of the dividend and divisor operands, the remainder is always no larger than the size of the division operation (32 bits in this case). Hence the remainder variable in this example is just a double word.
Before analyzing this code to see how it works, let's take a brief look at why a single 64/32 division will not work for this particular example even though the DIV instruction does indeed calculate the result for a 64/32 division. The naive approach, assuming that the x86 were capable of this operation, would look something like the following:
// This code does *NOT* work! mov( dividend[0], eax ); // Get dividend into edx:eax mov( divident[4], edx ); div( divisor, edx:eax ); // Divide edx:eax by divisor.Although this code is syntactically correct and will compile, if you attempt to run this code it will raise an ex.DivideError1 exception. The reason, if you'll remember how the DIV instruction works, is that the quotient must fit into 32 bits; since the quotient turns out to be $2_0000_091A, it will not fit into the EAX register, hence the resulting exception.
Now let's take another look at the former code that correctly computes the 64/32 quotient. This code begins by computing the 32/32 quotient of dividend[4]/divisor. The quotient from this division (2) becomes the H.O. double word of the final quotient. The remainder from this division (0) becomes the extension in EDX for the second half of the division operation. The second half divides edx:dividend[0] by divisor to produce the L.O. double word of the quotient and the remainder from the division. Note that the code does not zero extend EAX into EDX prior to the second DIV instruction. EDX already contains valid bits and this code must not disturb them.
The 64/32 division operation above is actually just a special case of the more general division operation that lets you divide an arbitrary sized value by a 32-bit divisor. To achieve this, you begin by moving the H.O. double word of the dividend into EAX and zero extending this into EDX. Next, you divide this value by the divisor. Then, without modifying EDX along the way, you store away the partial quotients, load EAX with the next lower double word in the dividend, and divide it by the divisor. You repeat this operation until you've processed all the double words in the dividend. At that time the EDX register will contain the remainder. The following program demonstrates how to divide a 128 bit quantity by a 32 bit divisor, producing a 128 bit quotient and a 32 bit remainder:
program testDiv128; #include( "stdlib.hhf" ) type t128:dword[4]; procedure div128 ( Dividend: t128; Divisor: dword; var QuotAdrs: t128; var Remainder: dword ); @nodisplay; const Quotient: text := "(type dword [edi])"; begin div128; push( eax ); push( edx ); push( edi ); mov( QuotAdrs, edi ); // Pointer to quotient storage. mov( Dividend[12], eax ); // Begin division with the H.O. dword. xor( edx, edx ); // Zero extend into EDX. div( Divisor, edx:eax ); // Divide H.O. dword. mov( eax, Quotient[12] ); // Store away H.O. dword of quotient. mov( Dividend[8], eax ); // Get dword #2 from the dividend div( Divisor, edx:eax ); // Continue the division. mov( eax, Quotient[8] ); // Store away dword #2 of the quotient. mov( Dividend[4], eax ); // Get dword #1 from the dividend. div( Divisor, edx:eax ); // Continue the division. mov( eax, Quotient[4] ); // Store away dword #1 of the quotient. mov( Dividend[0], eax ); // Get the L.O. dword of the dividend. div( Divisor, edx:eax ); // Finish the division. mov( eax, Quotient[0] ); // Store away the L.O. dword of the quotient. mov( Remainder, edi ); // Get the pointer to the remainder's value. mov( edx, [edi] ); // Store away the remainder value. pop( edi ); pop( edx ); pop( eax ); end div128; static op1: t128 := [$2222_2221, $4444_4444, $6666_6666, $8888_8888]; op2: dword := 2; quo: t128; rmndr: dword; begin testDiv128; div128( op1, op2, quo, rmndr ); stdout.put ( nl nl "After the division: " nl nl "Quotient = $", quo[12], "_", quo[8], "_", quo[4], "_", quo[0], nl "Remainder = ", (type uns32 rmndr ) ); end testDiv128; Program 4.2 Unsigned 128/32 Bit Extended Precision DivisionYou can extend this code to any number of bits by simply adding additional MOV / DIV / MOV instructions to the sequence. Like the extended multiplication the previous section presents, this extended precision division algorithm works only for unsigned operands. If you need to divide two signed quantities, you must note their signs, take their absolute values, do the unsigned division, and then set the sign of the result based on the signs of the operands.
If you need to use a divisor larger than 32 bits you're going to have to implement the division using a shift and subtract strategy. Unfortunately, such algorithms are very slow. In this section we'll develop two division algorithms that operate on an arbitrary number of bits. The first is slow but easier to understand, the second is quite a bit faster (in general).
As for multiplication, the best way to understand how the computer performs division is to study how you were taught to perform long division by hand. Consider the operation 3456/12 and the steps you would take to manually perform this operation:
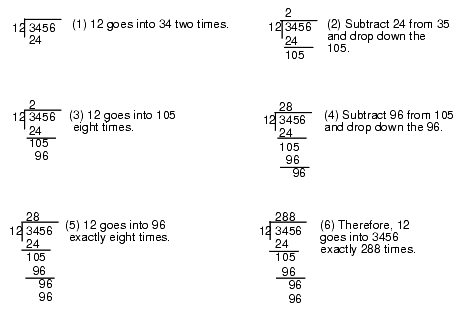
Figure 4.3 Manual Digit-by-digit Division Operation
This algorithm is actually easier in binary since at each step you do not have to guess how many times 12 goes into the remainder nor do you have to multiply 12 by your guess to obtain the amount to subtract. At each step in the binary algorithm the divisor goes into the remainder exactly zero or one times. As an example, consider the division of 27 (11011) by three (11):
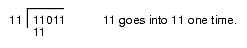
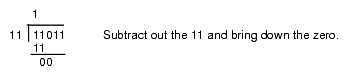
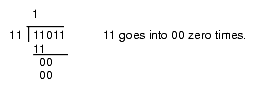

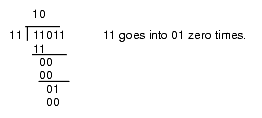

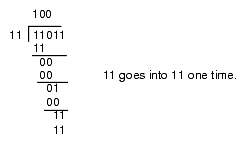
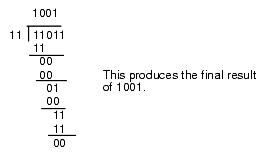
Figure 4.4 Longhand Division in Binary
There is a novel way to implement this binary division algorithm that computes the quotient and the remainder at the same time. The algorithm is the following:
Quotient := Dividend; Remainder := 0; for i:= 1 to NumberBits do Remainder:Quotient := Remainder:Quotient SHL 1; if Remainder >= Divisor then Remainder := Remainder - Divisor; Quotient := Quotient + 1; endif endforNumberBits is the number of bits in the Remainder, Quotient, Divisor, and Dividend variables. Note that the "Quotient := Quotient + 1;" statement sets the L.O. bit of Quotient to one since this algorithm previously shifts Quotient one bit to the left. The following program implements this algorithm
program testDiv128b; #include( "stdlib.hhf" ) type t128:dword[4]; // div128- // // This procedure does a general 128/128 division operation // using the following algorithm: // (all variables are assumed to be 128 bit objects) // // Quotient := Dividend; // Remainder := 0; // for i:= 1 to NumberBits do // // Remainder:Quotient := Remainder:Quotient SHL 1; // if Remainder >= Divisor then // // Remainder := Remainder - Divisor; // Quotient := Quotient + 1; // // endif // endfor // procedure div128 ( Dividend: t128; Divisor: t128; var QuotAdrs: t128; var RmndrAdrs: t128 ); @nodisplay; const Quotient: text := "Dividend"; // Use the Dividend as the Quotient. var Remainder: t128; begin div128; push( eax ); push( ecx ); push( edi ); mov( 0, eax ); // Set the remainder to zero. mov( eax, Remainder[0] ); mov( eax, Remainder[4] ); mov( eax, Remainder[8] ); mov( eax, Remainder[12]); mov( 128, ecx ); // Count off 128 bits in ECX. repeat // Compute Remainder:Quotient := Remainder:Quotient SHL 1: shl( 1, Dividend[0] ); // See the section on extended rcl( 1, Dividend[4] ); // precision shifts to see how rcl( 1, Dividend[8] ); // this code shifts 256 bits to rcl( 1, Dividend[12]); // the left by one bit. rcl( 1, Remainder[0] ); rcl( 1, Remainder[4] ); rcl( 1, Remainder[8] ); rcl( 1, Remainder[12]); // Do a 128-bit comparison to see if the remainder // is greater than or equal to the divisor. if ( #{ mov( Remainder[12], eax ); cmp( eax, Divisor[12] ); ja true; jb false; mov( Remainder[8], eax ); cmp( eax, Divisor[8] ); ja true; jb false; mov( Remainder[4], eax ); cmp( eax, Divisor[4] ); ja true; jb false; mov( Remainder[0], eax ); cmp( eax, Divisor[0] ); jb false; }# ) then // Remainder := Remainder - Divisor mov( Divisor[0], eax ); sub( eax, Remainder[0] ); mov( Divisor[4], eax ); sbb( eax, Remainder[4] ); mov( Divisor[8], eax ); sbb( eax, Remainder[8] ); mov( Divisor[12], eax ); sbb( eax, Remainder[12] ); // Quotient := Quotient + 1; add( 1, Quotient[0] ); adc( 0, Quotient[4] ); adc( 0, Quotient[8] ); adc( 0, Quotient[12] ); endif; dec( ecx ); until( @z ); // Okay, copy the quotient (left in the Dividend variable) // and the remainder to their return locations. mov( QuotAdrs, edi ); mov( Quotient[0], eax ); mov( eax, [edi] ); mov( Quotient[4], eax ); mov( eax, [edi+4] ); mov( Quotient[8], eax ); mov( eax, [edi+8] ); mov( Quotient[12], eax ); mov( eax, [edi+12] ); mov( RmndrAdrs, edi ); mov( Remainder[0], eax ); mov( eax, [edi] ); mov( Remainder[4], eax ); mov( eax, [edi+4] ); mov( Remainder[8], eax ); mov( eax, [edi+8] ); mov( Remainder[12], eax ); mov( eax, [edi+12] ); pop( edi ); pop( ecx ); pop( eax ); end div128; // Some simple code to test out the division operation: static op1: t128 := [$2222_2221, $4444_4444, $6666_6666, $8888_8888]; op2: t128 := [2, 0, 0, 0]; quo: t128; rmndr: t128; begin testDiv128b; div128( op1, op2, quo, rmndr ); stdout.put ( nl nl "After the division: " nl nl "Quotient = $", quo[12], "_", quo[8], "_", quo[4], "_", quo[0], nl "Remainder = ", (type uns32 rmndr ) ); end testDiv128b; Program 4.3 Extended Precision DivisionThis code looks simple but there are a few problems with it. First, it does not check for division by zero (it will produce the value $FFFF_FFFF_FFFF_FFFF if you attempt to divide by zero), it only handles unsigned values, and it is very slow. Handling division by zero is very simple, just check the divisor against zero prior to running this code and return an appropriate error code if the divisor is zero (or RAISE the ex.DivisionError exception). Dealing with signed values is the same as the earlier division algorithm, this problem appears as a programming exercise. The performance of this algorithm, however, leaves a lot to be desired. It's around an order of magnitude or two worse than the DIV/IDIV instructions on the x86 and they are among the slowest instructions on the CPU.
There is a technique you can use to boost the performance of this division by a fair amount: check to see if the divisor variable uses only 32 bits. Often, even though the divisor is a 128 bit variable, the value itself fits just fine into 32 bits (i.e., the H.O. double words of Divisor are zero). In this special case, that occurs frequently, you can use the DIV instruction which is much faster.
1Windows may translate this to an ex.IntoInstr exception.
|