2.12 Performance Improvements
The 80x86 microprocessors execute sequences of instructions at blinding speeds. Therefore, you'll rarely encounter a program that is slow which doesn't contain any loops. Since loops are the primary source of performance problems within a program, they are the place to look when attempting to speed up your software. While a treatise on how to write efficient programs is beyond the scope of this chapter, there are some things you should be aware of when designing loops in your programs. They're all aimed at removing unnecessary instructions from your loops in order to reduce the time it takes to execute one iteration of the loop.
2.12.1 Moving the Termination Condition to the End of a Loop
Consider the following flow graphs for the three types of loops presented earlier:
Initialization code Loop body Test for termination Code following the loopInitialization code Loop termination test Loop body Jump back to test Code following the loopInitialization code Loop body, part one Loop termination test Loop body, part two Jump back to loop body part 1 Code following the loopAs you can see, the REPEAT..UNTIL loop is the simplest of the bunch. This is reflected in the assembly language code required to implement these loops. Consider the following REPEAT..UNTIL and WHILE loops that are identical:
// Example involving a WHILE loop: mov( edi, esi ); sub( 20, esi ); while( esi <= edi ) do <<stmts>> inc( esi ); endwhile; // Conversion of the code above into pure assembly language: mov( edi, esi ); sub( 20, esi ); whlLbl: cmp( esi, edi ); jnle EndOfWhile; <<stmts>> inc( esi ); <<stmts>> jmp whlLbl; EndOfWhile: //Example involving a REPEAT..UNTIL loop: mov( edi, esi ); sub( 20, esi ); repeat <<stmts>> inc( esi ); until( esi > edi ); // Conversion of the REPEAT..UNTIL loop into pure assembly: rptLabel: <<stmts>> inc( esi ); cmp( esi, edi ); jng rptLabel;As you can see by carefully studying the conversion to pure assembly language, testing for the termination condition at the end of the loop allowed us to remove a JMP instruction from the loop. This can be significant if this loop is nested inside other loops. In the preceding example there wasn't a problem with executing the body at least once. Given the definition of the loop, you can easily see that the loop will be executed exactly 20 times. This suggests that the conversion to a REPEAT..UNTIL loop is trivial and always possible. Unfortunately, it's not always quite this easy. Consider the following HLA code:
while( esi <= edi ) do <<stmts>> inc( esi ); endwhile;In this particular example, we haven't the slightest idea what ESI contains upon entry into the loop. Therefore, we cannot assume that the loop body will execute at least once. So we must test for loop termination before executing the body of the loop. The test can be placed at the end of the loop with the inclusion of a single JMP instruction:
jmp WhlTest; TopOfLoop: <<stmts>> inc( esi ); WhlTest: cmp( esi, edi ); jle TopOfLoop;Although the code is as long as the original WHILE loop, the JMP instruction executes only once rather than on each repetition of the loop. Note that this slight gain in efficiency is obtained via a slight loss in readability. The second code sequence above is closer to spaghetti code that the original implementation. Such is often the price of a small performance gain. Therefore, you should carefully analyze your code to ensure that the performance boost is worth the loss of clarity. More often than not, assembly language programmers sacrifice clarity for dubious gains in performance, producing impossible to understand programs.
Note, by the way, that HLA translates its WHILE statement into a sequence of instructions that test the loop termination condition at the bottom of the loop using exactly the technique this section describes. Therefore, you do not have to worry about the HLA WHILE statement introducing slower code into your programs.
2.12.2 Executing the Loop Backwards
Because of the nature of the flags on the 80x86, loops which range from some number down to (or up to) zero are more efficient than any other. Compare the following HLA FOR loop and the code it generates:
for( mov( 1, J); J <= 8; inc(J)) do <<stmts>> endfor; // Conversion to pure assembly (as well as using a repeat..until form): mov( 1, J ); ForLp: <<stmts>> inc( J ); cmp( J, 8 ); jnge ForLp;Now consider another loop that also has eight iterations, but runs its loop control variable from eight down to one rather than one up to eight:
mov( 8, J ); LoopLbl: <<stmts>> dec( J ); jnz LoopLbl;Note that by running the loop from eight down to one we saved a comparison on each repetition of the loop.
Unfortunately, you cannot force all loops to run backwards. However, with a little effort and some coercion you should be able to write many FOR loops so they operate backwards. By saving the execution time of the CMP instruction on each iteration of the loop the code may run faster.
The example above worked out well because the loop ran from eight down to one. The loop terminated when the loop control variable became zero. What happens if you need to execute the loop when the loop control variable goes to zero? For example, suppose that the loop above needed to range from seven down to zero. As long as the upper bound is positive, you can substitute the JNS instruction in place of the JNZ instruction above to repeat the loop some specific number of times:
mov( 7, J ); LoopLbl: <<stmts>> dec( J ); jns LoopLbl;This loop will repeat eight times with J taking on the values seven down to zero on each execution of the loop. When it decrements zero to minus one, it sets the sign flag and the loop terminates.
Keep in mind that some values may look positive but they are negative. If the loop control variable is a byte, then values in the range 128..255 are negative. Likewise, 16-bit values in the range 32768..65535 are negative. Therefore, initializing the loop control variable with any value in the range 129..255 or 32769..65535 (or, of course, zero) will cause the loop to terminate after a single execution. This can get you into a lot of trouble if you're not careful.
2.12.3 Loop Invariant Computations
A loop invariant computation is some calculation that appears within a loop that always yields the same result. You needn't do such computations inside the loop. You can compute them outside the loop and reference the value of the computation inside the loop. The following HLA code demonstrates a loop which contains an invariant computation:
for( mov( 0, eax ); eax < n; inc( eax )) do mov( eax, edx ); add( j, edx ); sub( 2, edx ); add( edx, k ); endfor;Since j never changes throughout the execution of this loop, the sub-expression "j-2" can be computed outside the loop and its value used in the expression inside the loop:
mov( j, ecx ); sub( 2, ecx ); for( mov( 0, eax ); eax < n; inc( eax )) do mov( eax, edx ); add( ecx, edx ); add( edx, k ); endfor;Still, the value in ECX never changes inside this loop, so although we've eliminated a single instruction by computing the subexpression "j-2" outside the loop, there is still an invariant component to this calculation. Since we note that this invariant component executes n times in the loop, we can translate the code above to the following:
mov( j, ecx ); sub( 2, ecx ); intmul( n, ecx ); // Compute n*(j-2) and add this into k outside add( ecx, k ); // the loop. for( mov( 0, eax ); eax < n; inc( eax )) do add( eax, k ); endfor;As you can see, we've shrunk the loop body from four instructions down to one. Of course, if you're really interested in improving the efficiency of this particular loop, you'd be much better off (most of the time) computing k using the formula:
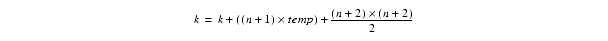
This computation for k is based on the formula:
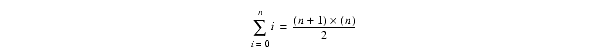
However, simple computations such as this one aren't always possible. Still, this demonstrates that a better algorithm is almost always better than the trickiest code you can come up with.
Removing invariant computations and unnecessary memory accesses from a loop (particularly an inner loop in a set of nested loops) can produce dramatic performance improvements in a program.
2.12.4 Unraveling Loops
For small loops, that is, those whose body is only a few statements, the overhead required to process a loop may constitute a significant percentage of the total processing time. For example, look at the following Pascal code and its associated 80x86 assembly language code:
FOR I := 3 DOWNTO 0 DO A [I] := 0;mov( 3, I ); LoopLbl: mov( I, ebx ); mov( 0, A[ebx*4] ); dec( I ); jns LoopLbl;Each iteration of the loop requires four instructions. Only one instruction is performing the desired operation (moving a zero into an element of A). The remaining three instructions control the repetition of the loop. Therefore, it takes 16 instructions to do the operation logically required by four.
While there are many improvements we could make to this loop based on the information presented thus far, consider carefully exactly what it is that this loop is doing-- it's simply storing four zeros into A[0] through A[3]. A more efficient approach is to use four MOV instructions to accomplish the same task. For example, if A is an array of dwords, then the following code initializes A much faster than the code above:
mov( 0, A[0] ); mov( 0, A[4] ); mov( 0, A[8] ); mov( 0, A[12] );Although this is a trivial example, it shows the benefit of loop unraveling. If this simple loop appeared buried inside a set of nested loops, the 4:1 instruction reduction could possibly double the performance of that section of your program.
Of course, you cannot unravel all loops. Loops that execute a variable number of times cannot be unraveled because there is rarely a way to determine (at assembly time) the number of times the loop will execute. Therefore, unraveling a loop is a process best applied to loops that execute a known number of times (and the number of times is known at assembly time.
Even if you repeat a loop some fixed number of iterations, it may not be a good candidate for loop unraveling. Loop unraveling produces impressive performance improvements when the number of instructions required to control the loop (and handle other overhead operations) represent a significant percentage of the total number of instructions in the loop. Had the loop above contained 36 instructions in the body of the loop (exclusive of the four overhead instructions), then the performance improvement would be, at best, only 10% (compared with the 300-400% it now enjoys). Therefore, the costs of unraveling a loop, i.e., all the extra code which must be inserted into your program, quickly reaches a point of diminishing returns as the body of the loop grows larger or as the number of iterations increases. Furthermore, entering that code into your program can become quite a chore. Therefore, loop unraveling is a technique best applied to small loops.
Note that the superscalar x86 chips (Pentium and later) have branch prediction hardware and use other techniques to improve performance. Loop unrolling on such systems many actually slow down the code since these processors are optimized to execute short loops.
2.12.5 Induction Variables
Consider the following modification of the loop presented in the previous section:
FOR I := 0 TO 255 DO csetVar[I] := {};Here the program is initializing each element of an array of character sets to the empty set. The straight-forward code to achieve this is the following:
mov( 0, i ); FLp: // Compute the index into the array (note that each element // of a CSET array contains 16 bytes). mov( i, ebx ); shl( 4, ebx ); // Set this element to the empty set (all zero bits). mov( 0, csetVar[ ebx ] ); mov( 0, csetVar[ ebx+4 ] ); mov( 0, csetVar[ ebx+8 ] ); mov( 0, csetVar[ ebx+12 ] ); inc( i ); cmp( i, 256 ); jb FLp;Although unraveling this code will still produce a performance improvement, it will take 1024 instructions to accomplish this task, too many for all but the most time-critical applications. However, you can reduce the execution time of the body of the loop using induction variables. An induction variable is one whose value depends entirely on the value of some other variable. In the example above, the index into the array csetVar tracks the loop control variable (it's always equal to the value of the loop control variable times 16). Since i doesn't appear anywhere else in the loop, there is no sense in performing all the computations on i. Why not operate directly on the array index value? The following code demonstrates this technique:
mov( 0, ebx ); FLp: mov( 0, csetVar[ ebx ]); mov( 0, csetVar[ ebx+4 ] ); mov( 0, csetVar[ ebx+8 ] ); mov( 0, csetVar[ ebx+12 ] ); add( 16, ebx ); cmp( ebx, 256*16 ); jb FLp;The induction that takes place in this example occurs when the code increments the loop control variable (moved into EBX for efficiency reasons) by 16 on each iteration of the loop rather than by one. Multiplying the loop control variable by 16 allows the code to eliminate multiplying the loop control variable by 16 on each iteration of the loop (i.e., this allows us to remove the SHL instruction from the previous code). Further, since this code no longer refers to the original loop control variable (i), the code can maintain the loop control variable strictly in the EBX register.
|